Introduction to RL

拾起Reinforcement Learning的基础概念和算法。

Terminology

强化学习中有很多的术语和概念，初学时经常被搞得很懵逼，所以先从术语开始，把基础的概念理解好。

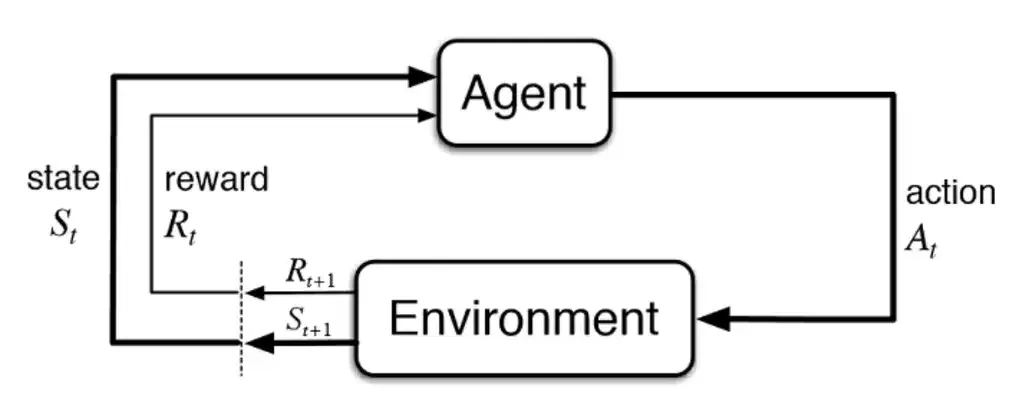
强化学习是一套框架，这套框架通用的描述一个可以执行动作的所谓Agent通过和环境的交互进行学习，框架图如下图所示： rl_framework

强化学习这套框架中充满了随机性，每一个概念几乎都是一个随机变量或概率密度函数，下面的开始的介绍中，简单规定一些符号：大写字母 $X$ 表示随机变量，小写字母 $x$ 表示随机变量的观测值，大写的 $P$ 概率密度函数，花体字母 $\mathcal{S}$ 表示集合。不同的教材对下面的概念会采用相当不同的符号表示，例如David Silver的课程，UCB的课程等，不同的符号系统随着概念和算法的深入公式会变得更困难，因此坚持一套符号表示即可。

Basics

Agent: Agent是环境中活动（执行动作）的主体，例如在真实世界中行驶的自动驾驶车（Ego Vehicle）。
Environment 环境或者现在的有些说法叫世界模型（World Model），是Agent所活动的环境的抽象。
State $S$ : 状态指的是当前Agent所包含的信息，这些信息决定着Agent的未来。在某时刻 $t$ 的状态 $S_t$ 是一个随机变量， $s_t$ 是当前时刻的观测值，可以有很多可能的 $s_t$ 。所有可能的状态的集合称为状态空间 $\mathcal{S}$ ，即State Space。
Action $A$ : 动作指的是Agent采取的动作。在某时刻 $t$ 的状态 $A_t$ 是一个随机变量， $a_t$ 是当前时刻的观测值，可以有很多可能的 $a_t$ ，这些动作可能是离散值，也可能是连续值。所有可能的动作的集合称为动作空间 $\mathcal{A}$ ，即Action Space。
Reward $R$ : 奖励指的是Agent采取了动作环境给予Agent的奖励值。在某时刻 $t$ 的状态 $R_t$ 是一个随机变量， $r_t$ 是当前时刻的观测值。奖励也会被称为奖励函数（reward function），环境根据当前的状态 $s_t$ 和采取的不同动作 $a_t$ ，会有不同的奖励值。

奖励也是一个很难的话题，因为RL是一个框架，Agent的目标是最大化未来的奖励，它塑造了Agent的学习目标和效率。很难有通用的奖励函数，一般是根据某个任务定义的，例如AlphaGo下棋，赢了得到了价值100的奖励，输了要惩罚100，这里奖励值的确定并没有科学的依据。例如在大语言模型应用强化学习进行RLHF，最大化的奖励是和人类对齐(alignment)的回答，但是模型也会出现Reward Hacking¹。

RL算法也经常会面临奖励稀疏(Sparse Reward)的问题，导致RL比较大的问题是学习低效(inefficient)，即需要超级大量的试错才能学到简单的动作。

Return $U$ : 回报的定义是累积的未来回报(Cumulative future reward)，注意是未来:

U_t=R_t+R_{t+1}+R_{t+2}+R_{t+3}+\cdots

由于未来时刻 $t$ 的奖励和当前比不一定等价，所以打个折扣 $\gamma$ ，也就是discounted return:

U_t=R_t+\gamma R_{t+1}+\gamma^2R_{t+2}+\gamma^3R_{t+3}+\cdots

需要注意的是 $U_t$ 是一个随机变量，它依赖于未来未观测到的奖励，而这些奖励依赖于未来采取的动作和状态，但是回报可以通过积分掉未观测到的变量获得期望值。

Trajectory: 轨迹是Agent与环境交互的序列： $s_1, a_1, r_1, s_2, a_2, r_2, \cdots$
State Transition: 状态转移 $p(\cdot \vert s, a)$ 指的是根据当前Agent的状态 $s$ 和采取的动作 $a$ ，环境转移到新状态 $s'$ 的概率，因此状态转移时一个概率密度函数 $p(s'\vert s,a)=P(S'=s' \vert S=s, A=a)$ 。

Policy Function

策略函数 $\pi$ 是RL中最重要的概念之一，是指Agent当前的状态 $s$ 映射到动作空间 $\mathcal{A}$ 内所有动作的概率分布，它控制Agent所采取的动作:

\pi(a \vert s)=P(A=a \vert S=s)

它是一个概率密度函数，所以有 $\sum_{a \in \mathcal{A}}\pi(a \vert s)=1$ 。

Value Functions

价值函数同样也是RL中最重要的概念之一，主要有动作-价值函数，以及状态-价值函数，两者有密切关系。 两个价值函数都是由策略函数Policy控制的期望，期望就是对未来回报的平均预期，比喻来说就是Agent的“经验”。

Action-Value Function

动作价值函数 $Q_{\pi}(s, a)$ ，即经常见到的 $Q$ 函数，描述了在给定状态 $s$ 下采取某个动作 $a$ 的好坏，这个好坏是通过代表未来累积奖励的回报 $U_t$ 的期望来进行评价的:

Q_{\pi}(s, a)=\mathbb{E}(U_t \vert S_t=s_t, A_t=a_t)

为什么是期望呢？因为未来（ $t+1$ 时刻之后）可能采取的动作和进入的状态都是随机变量，但是我们通过求期望，即通过概率加权求和或积分消掉未来的随机变量，从而大体知道可以预期的平均回报是多少。

$Q$ 函数依赖策略函数 $\pi(a \vert s)$ 和状态转移函数 $p(\cdot \vert s, a)$ 。

State-Value Function

状态价值函数 $V_{\pi}$ 衡量给定策略 $\pi$ ，当前状态的好坏，相当于对动作价值函数 $Q$ ，进一步积分掉所有的动作 $A$ ：

V_{\pi}=\mathbb{E}_{A\sim \pi(\cdot \vert s_t)}\big[Q_{\pi}(s_t, A) \big]=\int_{\mathcal{A}} \pi(a\vert s_t) \cdot Q_{\pi}(s_t,a) \, da

状态价值函数描述了给定策略 $\pi$ 现在所处的状态的好坏，不管采取什么动作。

Optimal Value Functions

最佳动作价值函数(Optimal action-value function)： $Q^*(s, a)$ 表示在策略函数 $\pi$ 和状态 $s$ 下采取动作 $a$ 的最大预期回报：

\begin{aligned} Q^*(s, a) &= \underset{\pi}{\text{max}} \, Q_{\pi}(s,a) \end{aligned}

最佳状态价值函数(Optimal state-value function)： $V^*(s)$ 表示在策略函数 $\pi$ 中当前状态 $s$ 的最大预期回报：

V^{*}(s) = \underset{\pi}{\text{max}} \, V_{\pi}(s)

可以看到，两个最佳价值函数（ $Q^*(s,a)$ 和 $V^*(s)$ ）都和策略函数 $\pi$ 有关，即只要找到最佳的策略函数 $\pi^*(a\vert s)$ ：

\pi \geq \pi' \quad \text{if} \, V_{\pi}(s) \geq V_{\pi'}(s) , \forall s

对任意马尔科夫决策过程MDP有定理：

一定有一个最佳策略 $\pi^*(a\vert s)$ 好于或等于其他所有的策略
最优策略一定实现最优状态价值函数， $V_{\pi^*}(s) \geq V^*(s), \forall \pi$
最优策略一定实现最优动作价值函数， $Q_{\pi^*}(s,a) \geq Q^*(s,a), \forall \pi$

RL算法的目标是最大化未来累积回报，可以看到，如果已知最优价值函数或最优策略，都可以实现RL这一目标，因此RL算法主要分为Value-based和Policy-based的方法。

Policy-based Method

Policy-based方法，例如Policy Gradient，是直接建模策略函数 $\pi(a\vert s; \theta)$ 来实现最大化未来累积回报的预期：

\text{maximize} \, \mathcal{J}(\theta)=V_{\pi_{\theta}}(S_1)= \mathbb{E}_{\pi_{\theta}}[V_1]

其中， $S_1$ 是初始状态。

期望累积奖励可以表示为平稳分布下的期望²：

\mathcal{J}(\theta)=\sum_{s\in \mathcal{S}}d_{\pi_{\theta}}(s)V_{\pi_{\theta}}(s)=\sum_{s\in \mathcal{S}}\big(d_{\pi_{\theta}}(s)\sum_{a\in \mathcal{A}}\pi(a\vert s,\theta)Q_{\pi}(s,a) \big)

其中， $d_{\pi_{\theta}}(s)$ 称为平稳分布(stationary distribution)。

Policy Gradient

对上面的目标函数解析的求梯度(这里参考的是Wang Shusen的简化版）：

\begin{aligned} \frac{\partial \mathcal{J}(\theta)}{\partial \theta}&=\frac{\partial \sum_{s\in \mathcal{S}}d(s)\sum_{a}\pi(a\vert s;\theta)\cdot Q_{\pi}(s,a)}{\partial \theta} \\ &=\sum_{s\in \mathcal{S}}d(s)\sum_{a\in\mathcal{A}} \frac{\partial \pi(a\vert s;\theta)\cdot Q_{\pi}(s,a)}{\partial \theta} \\ &=\sum_{s\in \mathcal{S}}d(s)\sum_{a} \frac{\partial \pi(a\vert s;\theta)}{\partial \theta}\cdot Q_{\pi}(s,a) \quad \text{via}\nabla f(x)=f(x)\nabla\log f(x)\\ &=\sum_{s\in \mathcal{S}}d(s)\sum_{a}\pi(a\vert s;\theta) \frac{\partial \log \pi(a\vert s;\theta)}{\partial \theta}\cdot Q_{\pi}(s,a) \quad \text{via} \sum_{s\in \mathcal{S}}d(s)=1 \\ &=\mathbb{E}_{\mathcal{A}}\big[\frac{\partial\log\pi(A\vert s;\theta)}{\partial \theta}\cdot Q_{\pi}(s,A) \big] \\ &=\mathbb{E}_{\mathcal{A}}[\nabla_{\theta} \log\pi(A\vert s;\theta)\cdot Q_{\pi}(s,A)] \end{aligned}

$\nabla_{\theta}\mathcal{J}(\theta)$ 称为策略梯度(Policy gradient)，注意的是它是一个期望值，请记住这个公式。

Score Function

score function（评分函数）定义为对数似然函数关于参数的梯度，这个不太像是人话，直白的说就是有一个概率分布 $p(x;\theta)$ ，它的参数是 $\theta$ ，想要关于参数 $\theta$ 求导：

s(\theta)=\nabla_{\theta}\log p(x;\theta)

核心性质：

期望为零： $\mathbb{E}[s(\theta)]=0$ ，即微小的变化对score的平均影响为 $0$
方差与Fisher information： $Var[s(\theta)]$ 称为Fisher information, 用于衡量参数估计的精度

策略梯度的核心是梯度。

PS: 策略梯度中的 $\nabla_{\theta} \log\pi(A\vert s;\theta)$ 即为策略函数 $\pi(a\vert s;\theta)$ 的score function。

PS2: 为什么叫score function这么奇怪的名字？LLM给出的解释是：梯度指示了参数空间中“得分”增长最快的方向，量化评分参数的合理程度，得分越高，参数越合理。

另外，生成模型中的score-based model，和上面有一些不同，score-based model是指数据分布的对数概率梯度： $s(x)=\nabla_{x}\log p(x)$

Gradient Ascent

策略梯度算法使用梯度上升来更新参数(梯度下降用于最小化目标函数，对应的梯度上升用来最大化目标函数)，伪代码如下：

从环境中得到状态 $s_t$
从策略函数 $\pi(\cdot\vert s_t;\theta)$ 中随机抽样出 $a_t$
计算 $q_t \approx Q_{\pi}(s_t, a_t)$ $\leftarrow$ 下文回讲如何计算 $q_t$
求梯度: $\mathbb{d}_{\theta, t}=\frac{\partial \log\pi(\red{a_t}\vert s_t, \theta)}{\partial \theta} \big\vert_{\theta=\theta_t}$
(近似)计算policy gradient: $\mathbf{g}(\red{a_t},\theta_t)=q_t\cdot \mathbb{d}_{\theta, t}$ $\leftarrow$ 这里是使用蒙特卡洛近似，只使用一次随机采样来估计policy gradient(回想一下policy gradient是期望)
更新模型参数： $\theta_{t+1}=\theta_t + \beta \cdot \mathbf{g}(\red{a_t},\theta_t)$

使用蒙特卡洛近似的方法对policy gradient是无偏估计，但是它的缺点是方差高。

还有一个问题：如何求 $Q_{\pi}(s_t, a_t)$ ？使用REINFORCE方法:

使用当前的策略函数 $\pi$ 执行直到结束，收集轨迹： $s_1, a_1, r_1, s_2, a_2, r_2, \cdots, s_T, a_T, r_T$
计算 $u_t=\sum_{k=t}^{T}\gamma^{k-t}r_k$
因为 $Q_{\pi}(s_t,a_t)=\mathbb{E}[U_t]$ ，我们使用 $u_t$ 来近似 $Q_{\pi}(s_t,a_t)$

REINFORCE还有一个样本效率低的问题：执行当前策略 $\pi_{old}$ 收集到的轨迹后，更新参数得到了策略函数 $\pi_{new}$ ，这时之前收集到的轨迹就完全没有办法使用了。REINFORCE属于严格的on-policy算法。

另外一个方法是使用一个网络来近似 $Q_{\pi}(s_t, a_t)$ ，这个就属于Actor-Critic方法了，在后面小节进行。

Policy Gradient with Baseline

前述使用MC采样的Policy Gradient算法的问题是方差较高，学者引入Baseline技巧，可以实现降低方差的作用。

首先来看一个推导：

\begin{aligned} \quad &\mathbb{E}_{A\sim \pi}[\blue{b}\cdot \nabla_{\theta} \log\pi(A\vert s;\theta)] \\ =& \blue{b} \cdot \mathbb{E}_{A\sim \pi}[\nabla_{\theta} \log\pi(A\vert s;\theta)] \\ =& \blue{b} \cdot \sum_{a}\pi(a\vert s;\theta) [\frac{\partial \log \pi(a\vert s;\theta)}{\partial \theta}] \quad \text{via }\frac{d}{dx} \log(f(x)) = \frac{1}{x}f'(x)\\ =& \blue{b} \cdot \sum_{a} \cancel{\pi(a\vert s;\theta)}[\frac{1}{\cancel{\pi(a\vert s;\theta)}}\cdot \frac{\partial \pi(a\vert s;\theta)}{\partial \theta}] \\ =& \blue{b} \cdot \frac{\partial\sum_{a}\pi(a\vert s;\theta)}{\partial \theta} \\ =& \blue{b} \cdot \frac{\partial 1}{\partial \theta} \\ =& 0 \end{aligned}

$b$ 就是baseline，只要 $b$ 和求导的参数 $\theta$ 以及动作 $a$ 无关，它的期望就是 $0$ ，所以把上式添加到Policy Gradient中，不改变Policy Gradient的期望值：

\begin{aligned} PG =& \mathbb{E}_{\mathcal{A}}\big[\nabla_{\theta} \log\pi(A\vert s;\theta) \cdot Q_{\pi}(s,A) \big] \\ =& \mathbb{E}_{\mathcal{A}}\big[\nabla_{\theta} \log\pi(A\vert s;\theta) \cdot Q_{\pi}(s,A) - \nabla_{\theta} \log\pi(A\vert s;\theta)\cdot\blue{b}\big] \\ =& \mathbb{E}_{\mathcal{A}}[\nabla_{\theta} \log\pi(A\vert s;\theta)\cdot(Q_{\pi}(s,A)-\blue{b})] \end{aligned}

其中， $A(s,a)=Q_{\pi}(s,a)-\blue{b}$ 又称为Advantage函数。

但是为什么要加呢？虽然不改变期望值，但是在使用蒙特卡洛近似(随机采样 $a_t$ 并计算 $g_t$ )时，选择合适的baseline，可以降低方差。baseline的选择有很多， $b$ 可以为常数，更常见的选择是 $b=V(s)$ ，即 $A(s,a)=Q_{\pi}(s,a)-\blue{b}=Q_{\pi}(s,a)-V_{\pi}(s)$ 。直观的解释Advantange函数的话就是：

$A(s,a) > 0$ ，则表示当前动作 $a$ 的回报优于平均值
$A(s,a) < 0$ ，则表示当前动作 $a$ 的回报低于平均值

TRPO

TRPO全称是Trust Region Policy Optimization，是优化策略函数的方法，将数值优化领域的Trust Region优化巧妙应用到策略函数的优化。

Trust Region

单独拿出来Trust Region是因为这不是TRPO的发明，而是数值优化领域的算法，首先理解Trust Region的基础，可以更好的理解TRPO。这里推荐Wang Shusen老师的视频TRPO 置信域策略优化，非常清晰。

假设 $\mathcal{N}(\theta_{\text{old}})$ 是参数 $\theta_{\text{old}}$ 的邻域，即这个邻域内的参数距离 $\theta_{\text{old}}$ 在一定的距离之内，度量距离有多种选择，例如KL散度。如果我们有一个函数， $L(\theta \vert \theta_{\text{old}})$ 在 $\mathcal{N}(\theta_{\text{old}})$ 内近似 $\mathcal{J}(\theta)$ ，那么称 $\mathcal{N}(\theta_{\text{old}})$ 为Trust Region。

Trust Region算法重复两件事情：

Approximation: 给定当前参数 $\theta_{old}$ ，构建 $L(\theta \vert \theta_{\text{old}})$ ，它是在邻域 $\mathcal{N}(\theta_{\text{old}})$ 内对目标函数 $J(\theta)$ 的近似
Maximization: 在Trust Region，更新参数 $\theta_{\text{new}}$ : $\theta_{\text{new}} \leftarrow \underset{\theta \in \mathcal{N}(\theta_{\text{old}})}{\text{argmax}}\,L(\theta\vert \theta_{\text{old}})$

TR Policy Optimization

首先，重新改写目标函数 $\mathcal{J}(\theta)$ ，其中的技巧是重要性采样:

\begin{aligned} \mathcal{J}(\theta) &= \mathbb{E}_{S}[V_{\pi}(S)] \\ &= \mathbb{E}_{S}\big[\sum_{a}\pi(a\vert s;\theta)\cdot Q_{\pi}(s,a)] \\ &= \mathbb{E}_{S}\big[\pi(a\vert s;\theta_{\text{old}}) \cdot \frac{\pi(a\vert s;\theta)}{\pi(a\vert s;\theta_{\text{old}})} \cdot Q_{\pi}(s,a) \big] \\ &= \mathbb{E}_{S}\Big[\mathbb{E}_{A \sim \pi(\cdot\vert s;\theta_{\text{old}})}\big[\frac{\pi(a\vert s;\theta)}{\pi(a\vert s;\theta_{\text{old}})} \cdot Q_{\pi}(s,a) \big]\Big] \\ &= \mathbb{E}_{S,A}\big[\frac{\pi(A\vert S;\theta)}{\pi(A\vert S;\theta_{\text{old}})} \cdot Q_{\pi}(S,A) \big] \end{aligned}

TRPO论文中是使用Advantage函数来替代 $Q$ 函数的，公式推导和理解上差异不大，这里与Wang Shushen老师的课程中的公式一致。

$\theta_{\text{old}}$ 是什么？

理解 $\theta_{\text{old}}$ 需要理解策略梯度的训练过程：

Rollout（数据收集）：由于TRPO的on-policy特性，每次更新梯度，需要使用当前参数( $\theta_{\text{old}}$ )的策略与环境交互，得到轨迹数据，这些数据用于使用梯度上升进行参数更新；为了加快rollout，gym环境使用Vectorized Environments并行化的模拟
使用Rollout得到的数据作为训练数据训练policy，因此公式中的 $\theta$ 就是当前的正要更新的模型参数，因为要支持多轮的梯度更新，使用的都是同一批使用 $\theta_{\text{old}}$ 得到的轨迹数据，这里应该可以更好的理解为什么写为 $\theta_{\text{old}}$ ：

rollout_data = agent.policy_rollout()
for epoch in range(update_epochs):
    obs_old, actions_old, logprobs_old = sample_rollout_actions(rollout_data)
    new_action, new_value = \
        agent.get_action_value(obs_old, actions_old)
    logratio = logprobs_new - logprobs_old
    ratio = logratio.exp() # \pi(\theta) / \pi(\theta_old)
    # ... gradient ascent

在做重要性采样时，如果提议分布和目标分布差异过大，是没有办法进行优化的，因此我们假设的也是当前策略函数的分布 $\theta_{\text{old}}$ 和将要优化的策略函数的分布非常的近似，因此在Trust Region小步更新，更新步长太大也会造成优化不稳定。

下面开始应用Trust Region的两步(Approximation和Maximization)来优化目标函数：

Step 1. Approximation: 在参数 $\theta_{\text{old}}$ 的邻域内构建 $L(\theta\vert \theta_{\text{old}})$ 近似 $\mathcal{J}(\theta)=\mathbb{E}_{S,A}\big[\frac{\pi(A\vert S;\theta)}{\pi(A\vert S;\theta_{\text{old}})} \cdot Q_{\pi}(S,A) \big]$

由于 $S$ 和 $A$ 都是状态和动作的随机变量，可以从状态转移函数和 $\pi$ 函数中随机采样得到，使用 $\pi(A\vert s;\theta_{\text{old}})$ 和概率转移函数得到一组轨迹： $s_1,a_1,r_1,s_2,a_2,r_2,\cdots,s_n,a_n,r_n$ ，这些轨迹点相当于是训练策略函数 $\pi_{\theta}$ 的训练数据。使用这组轨迹（蒙特卡洛）近似 $\mathcal{J}(\theta)$ :

\mathcal{J}(\theta)\approx L(\theta\vert\theta_{old})=\frac{1}{n}\sum_{i=1}^{n}\frac{\pi(a_i\vert s_i;\theta)}{\pi(a_i\vert s_i;\theta_{old})}\cdot Q_{\pi}(s_i,a_i)

上式中， $Q_{\pi}(s_i,a_i)$ 可以使用REINFORCE方法用roll out的轨迹进行估计，即 $u_i$ ，则：

\tilde{L}(\theta\vert\theta_{old})=\frac{1}{n}\sum_{i=1}^{n}\frac{\pi(a_i\vert s_i;\theta)}{\pi(a_i\vert s_i;\theta_{old})}\cdot u_i

Step 2. Maximization: 在Trust Region，更新参数 $\theta_{\text{new}}$ :

\theta_{\text{new}} \leftarrow \underset{\theta \in \mathcal{N}(\theta_{\text{old}})}{\text{argmax}}\,\tilde{L}(\theta\vert \theta_{\text{old}}); \quad \text{s.t.} \theta\in \mathcal{N}(\theta_{\text{old}})

这是一个带约束的优化问题，求解这个问题比较复杂，可以简单理解一个二阶优化问题，即使用到了Hessian矩阵。因此，后续PPO对此进行了改进。

PPO

近端策略优化算法是对TRPO算法的改进，TRPO有训练稳定的优点，但是使用二阶计算量较大。 PPO是对TRPO的改进，主要是对比较复杂的带约束的最优化问题进行了简化，可以使用一阶的优化算法进行，大大加快了效率。

我们回顾一下TRPO的带约束的优化问题：

\begin{aligned} &\underset{\theta}{\text{maximize}} \quad \mathbb{E}\big[\frac{\pi(a\vert s;\theta)}{\pi(a\vert s;\theta_{\text{old}})}A_{\pi_{\text{old}}}(s,a) \big] \\ &\text{s.t.} \quad \mathbb{E}[D_{KL}(\pi_{\theta_{\text{old}}}(\cdot\vert s) \parallel \pi_{\theta}(\cdot \vert s))] \leq \delta \end{aligned}

PPO算法有两个变体，相对TRPO来说都很简洁，它们是 $\text{PPO}^{KLPEN}$ 和 $\text{PPO}^{CLIP}$ ，其中 $\text{PPO}^{CLIP}$ 效果更好，更常见。

PPO Penalty

$\text{PPO}^{KLPEN}$ ，把约束项 $D_{KL}$ 放入到目标函数中去（有些类似拉格朗日乘子法），就变成了无约束的优化问题，这样就可以直接使用各种一阶优化算法了，例如SGD，ADAM：

\mathbb{E}\big[\frac{\pi(a\vert s;\theta)}{\pi(a\vert s;\theta_{\text{old}})}A_{\pi_{\text{old}}}(s,a) \big] - \beta \cdot \mathbb{E}[D_{KL}(\pi_{\theta_{\text{old}}}(\cdot\vert s) \parallel \pi_{\theta}(\cdot \vert s))]

其中的 $\beta$ 是一个自适应的调整项，需要一个作为超参数的 $d_{\text{target}}$ ，首先计算 $d=\mathbb{E}[D_{KL}(\pi_{\theta_{\text{old}}}(\cdot\vert s) \parallel \pi_{\theta}(\cdot \vert s))]$ :

如果 $d < d_{\text{target}} / 1.5 \rightarrow \beta=\beta / 2$
如果 $d > d_{\text{target}} \times 1.5 \rightarrow \beta=\beta \times 2$

PPO CLIP

$\text{PPO}^{CLIP}$ 对Trust Region的进行了简化，通过控制重要性采样比率控制更新的补偿。令重要性采样比率为 $r(\theta)=\frac{\pi(a;\theta)}{\pi(a;\theta_{\text{old}})}$ ，对 $r(\theta)$ 进行截断，并选择最小（“悲观”）的那一项：

L^{CLIP}(\theta)=\mathbb{E}[\text{min}(r(\theta)A_{\pi_{\text{old}}}(s,a), \text{clip}(r(\theta), 1-\epsilon, 1+\epsilon))A_{\pi_{\text{old}}}(s,a)]

$\text{PPO}^{CLIP}$ 是更常见的目标函数，论文的实验中也有更好的表现。

PPO论文作者在第5节中提到，很多方法会使用一个网络来估计advantage函数中的 $V_{\pi}(s)$ ，如果policy网络和value网络共享参数，需要增加价值函数项 $L^{VF}$ 和熵奖励项(Entropy Bonus) $S$ ，写作：

L^{CLIP+VF+S}=\mathbb{E}[L^{CLIP}(\theta)-c_1L^{VF}(\theta)+c_2S[\pi_{\theta}(s)]]

其中的 $c_1, c_2$ 都是超参数，其他两项：

$L^{VF}=(V_{\theta}(s)-V^{target})^2$ ， $V^{target}$ 可以通过广义优势估计(General Advantage Estimation, GAE)得到。
$S[\pi_{\theta}(s)]=\mathbb{E}[-\pi_{\theta}(a\vert s)\log \pi_{\theta}(a\vert s)]$ ，这一公式是从熵的定义中来，熵越大表明信息量越大，目标函数鼓励这一项更大（因为使用的是 $+$ 号），可以估计模型增加探索，因为 $\pi$ 函数控制动作。

PPO的算法的实现³有非常多的细节和技巧，对于复现PPO算法很重要，有博客⁴总结了PPO实现的各种细节，会再另外一篇博客中单独叙述。

Valued-based Method

Value函数的定义即为对未来回报的期望，因此直接使用函数来近似动作/状态价值函数(Value Functions)称为基于价值函数的算法。

DQN

深度学习时代，经典的Deep Q Network就是使用深度网络 $Q(s,a ;\mathbf{w})$ 来近似动作价值函数 $Q(s,a)$ ，并用来控制Agent的动作：

a_t=\underset{a}{\text{argmax}} \, Q(s_t, a;\mathbf{w})

每次贪心地选择最大化价值的动作，则得到最佳动作-价值函数 $Q^*(s,a)$ 。

我们不对DQN的网络做过多解读，举一个简单的打马里奥的例子，游戏的动作动作是 $\mathcal{A}=[\text{left}, \text{right}, \text{up}]$ ，网络的输入是当前的图像，输出是每个动作的价值，例如 $[200, 100, 150]$ ，每次选择最大价值的动作。

Temporal Difference

如何训练DQN呢？ 一般使用TD Learning进行训练。

RL是时序决策框架，通常以一个片段(episode)为基础，即一定会包含终止的状态。在某时刻 $t$ ，使用 $Q(s_t, a;\mathbf{w})$ 来估计不同动作的未来预期回报，但是什么时候才会得到未来预期回报的真值(GroundTruth)呢？那显然得得等到这个片段结束才会知道真值，使用梯度下降来更新模型参数，这样效率就会比较低下。

能不能在片段没有结束之前进行更新模型参数呢？可以，因为经过了某些步数之后，获得了这部分奖励的真值，可以使用这部分的真值来更新最初的预测，即每一步都修正之前的预测，每一步都更新模型的参数。

回报 $U_t$ 包含一定的递归属性： $U_t=R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \gamma^3 R_{t+3} + \cdots=R_t + \gamma U_{t+1}$ 。

把上面关于 $U_t$ 的递归方程应用在DQN中：

\underbrace{Q(s_t,a;\mathbf{w})}_{\text{Estimate of }U_t} \approx \mathbb{E}[r_t+\gamma\cdot \underbrace{Q(S_{t+1}, A_{t+1}; \mathbf{w})]}_{\text{Estimate of }U_{t+1}}

把求期望括号内的部分称为TD Target:

\underbrace{Q(s_t,a;\mathbf{w})}_{\text{Prediction}} \approx \mathbb{E}\underbrace{[r_t+\gamma\cdot Q(S_{t+1}, A_{t+1}; \mathbf{w})]}_{\text{TD Target}}

有了Prediction和Target，就可以构建常见的损失函数更新模型参数了，令：

\begin{aligned} y_t &= r_t + \gamma \cdot Q(s_{t+1},a_{t+1};\mathbf{w_t}) \\ &= r_t + \gamma \cdot \underset{a}{\text{max}}Q(s_{t+1}, a; \mathbf{w_t}) \end{aligned}

损失函数即为：

L = \frac{1}{2}[Q(s_{t},a_{t};\mathbf{w_t})-y_t]^2

梯度更新参数：

\mathbf{w_{t+1}=\mathbf{w_t}-\alpha\cdot\frac{\partial L}{\partial w}\Big\vert_{w=w_t}}

使用TD训练DQN的伪代码：

获得状态 $S_t=s_t$ ，执行动作 $A_t=a_t$
预测价值： $q_t=Q(s_t,a_t;\mathbf{w_t})$
求微分： $\mathbf{d_t}=\frac{\partial Q(s_t,a_t;\mathbf{w_t})}{\partial \mathbf{w_t}} \big \vert_{w=w_t}$
环境提供下一个状态 $s_{t+1}$ 和当前的奖励 $r_t$
计算TD Target： $y_t=r_t + \gamma \cdot \underset{a}{\text{max}}Q(s_{t+1}, a; \mathbf{w_t})$
使用梯度下降更新参数： $\mathbf{w_{t+1}}=\mathbf{w_t}-\alpha\cdot (q_t-y_t) \mathbf{d}_t$

Actor-Critic Method

Actor-Critic Method是Value-based和Policy-based的结合，即使用模型同时对策略函数 $\pi(a \vert s; \mathbf{\theta})$ 和动作-价值函数 $Q_{\pi}(a,s;\mathbf{w})$ 进行建模。在前面Policy Gradient的训练处已经提到使用模型来估计 $Q$ 函数。

Actor指的是策略函数 $\pi(a \vert s; \mathbf{\theta})$ ，用来控制动作的输出，Critic指的是动作-价值函数 $Q_{\pi}(a,s;\mathbf{w})$ ，用来对采取的动作进行打分，两者同时训练，使得Agent对动作的预期回报的估计越来越准，也更有可能得到更好的动作：

V_{\pi}(s)=\sum_a \pi(a \vert s; \mathbf{\theta}) \cdot Q_{\pi}(a,s;\mathbf{w})

Training Actor-Critic

同时训练策略函数 $\pi(a \vert s; \mathbf{\theta})$ 和动作-价值函数 $Q_{\pi}(a,s;\mathbf{w})$ ，需要分别用到前面的TD和梯度上升，伪代码如下：

获得状态 $s_t$
根据 $\pi(a \vert s; \mathbf{\theta})$ 随机采样动作 $a_t$
执行动作 $a_t$ ，从环境中获得奖励 $r_t$ ，并转移到下一个状态 $s_{t+1}$
使用TD更新Critic网络参数 $\mathbf{w}$ $w$
1. 从 $\pi(\cdot \vert s_{t+1}; \mathbf{\theta})$ 采样动作 $\tilde a_{t+1}$ ，但是并不执行 $\tilde a_{t+1}$
2. 使用 $Q_{\pi}(a,s;\mathbf{w})$ 来计算： $q_t=Q(s_t, a_t;\mathbf{w_t})$ 和 $q_{t+1}=Q(s_{t+1}, \tilde a_{t+1}; \mathbf{w_t})$
3. 计算TD target: $y_t=r_t+\gamma \cdot q_{t+1}$
4. 损失函数： $L(\mathbf{w})=\frac{1}{2}[q_t-y_t]^2$
5. 梯度下降更新参数： $\mathbf{w_{t+1}}=\mathbf{w_t}-\alpha \cdot \frac{\partial L(\mathbf{w_t})}{\partial \mathbf{w}} \big |_{\mathbf{w}=\mathbf{w_t}}$
使用policy gradient来更新参数 $\mathbf{\theta}$ $θ$
1. 计算梯度: $\mathbb{d}_{\theta, t}=\frac{\partial \log\pi(a_t \vert s_t, \theta)}{\partial \theta} \big\vert_{\theta=\theta_t}$
2. 更新参数： $\mathbf{\theta_{t+1}}=\mathbf{\theta}+\beta \cdot q_t \cdot \mathbb{d}_{\theta, t}$
重复直到收敛

Policy vs Value vs Actor-Critic

方法	优点	缺点
Policy-based	1.直接优化策略函数，适合连续动作空间 2.支持随机策略（从策略函数中采样得到动作）	1.高方差，训练不稳定 2.采样效率低（on-policy），收敛速度慢 3.可能陷入局部最优，对超参敏感
Value-based	1.采样效率高：经验回放复用样本 2.确定性策略，通过价值函数选择最佳动作 3.收敛性较好	1.无法处理连续动作空间 2.确定性策略函数灵活性差 3.Q-learning的max操作导致价值函数高估
Actor-Critic	1.结合Policy和Value方法，平衡探索与利用(随机/确定性策略) 2.低方差，Critic估计逼policy方法方差更低 3.可处理连续和离散动作空间	1.训练难度高，同时训练两个网络，调参难度大 2.Critic估计的误差可能误导Actor 3.依赖Critic估计的准确性

MISC

on-policy v.s off-policy

名称	on-policy	off-policy
定义	行为策略(生成数据的策略)和目标策略(正在被优化的策略)必须是同一个策略	行为策略和目标策略不是同一个策略
特性	1.必须用当前策略与环境交互(rollout)的数据使用策略更新 2.策略更新后之前的数据被扔掉，样本效率低	1.可复用历史数据，样本效率高 2.行为策略可以更自由(如更注重探索)，而目标策略更注重优化 3.数据来自不同策略，需处理分布的差异
算法	典型算法：REINFORCE, SARSA, PPO	典型算法：Q-Learnig, DQN, DDPG

model-free v.s model-based

model-based方法：

显式地学习动态模型，即转移函数 $P(s' \vert s, a)$ 和奖励函数 $R(s,a)$ ，利用该模型进行规划(Planning)，例如通过模拟环境预测未来状态，从而优化策略或价值函数
特点：依赖环境模型，通过模型生成的虚拟轨迹来辅助决策
典型算法：Monte Carlo Tree Search (MCTS)（如AlphaGo中的规划方法），Dyna-Q, PILCO

model-free方法：

不显式地学习动态模型，直接通过试错从经验中学习策略或价值函数，依赖与环境的实时交互数据，而非通过动态模型的预测
特点：不依赖动态模型，数据驱动，样本效率低，需要海量的交互数据；这也是目前主流的算法方向
典型算法：Q-Learning, DQN，REINFORCE， PPO，A3C

Terminology

Basics

Policy Function

Value Functions

Action-Value Function

State-Value Function

Optimal Value Functions

Policy-based Method

Policy Gradient

Gradient Ascent

Policy Gradient with Baseline

TRPO

Trust Region

TR Policy Optimization

PPO

PPO Penalty

PPO CLIP

Valued-based Method

DQN

Temporal Difference

Actor-Critic Method

Training Actor-Critic

Policy vs Value vs Actor-Critic

MISC

on-policy v.s off-policy

model-free v.s model-based

Footnotes